Arbore Partial De Cost Minim

Dacă graful nu este conex atunci algoritmul găsește o pădure parțială de cost minim un.

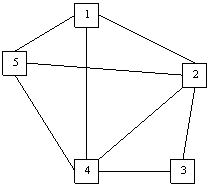
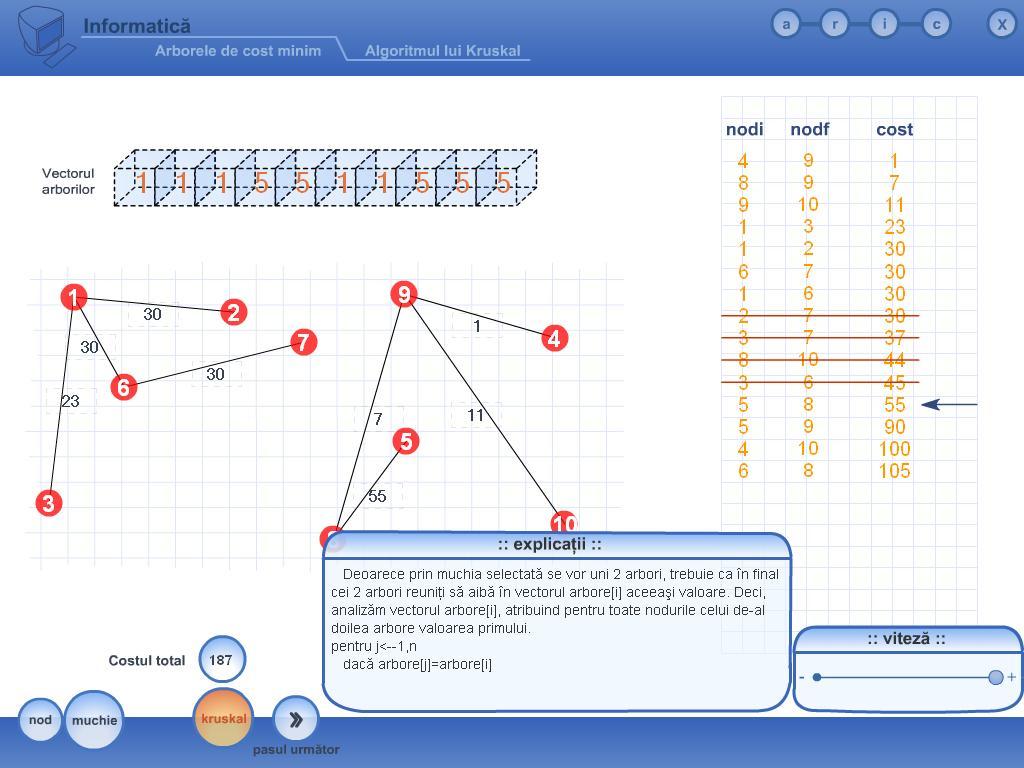
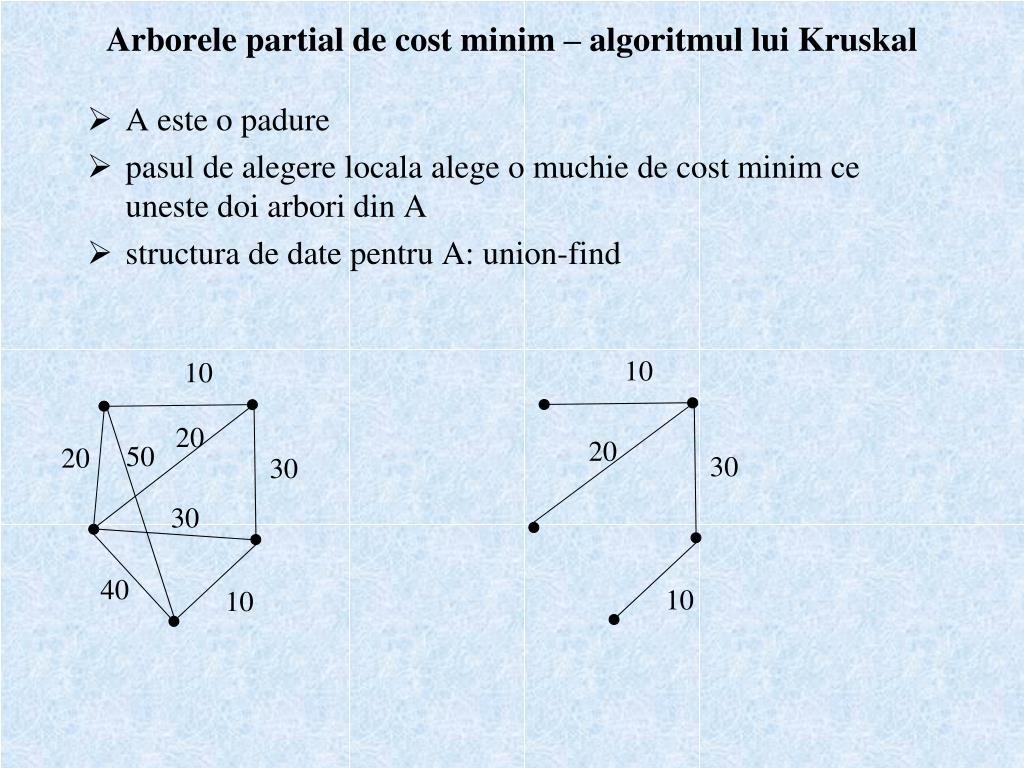
Arbore partial de cost minim. Algoritmul lui kruskal este un algoritm în teoria grafurilor care găsește arborele parțial de cost minim pentru un graf conex ponderat. Se cere sa se aleaga o parte din muchii astfel incat se asigure existenta unui lant intre oricare doua orase si costul total sa fie minim. Fie g x u un graf conex în care fiecare muchie are atașat un cost. Un arbore partial de cost minim pentru graful dat poate fi format din urmatoarele muchii.

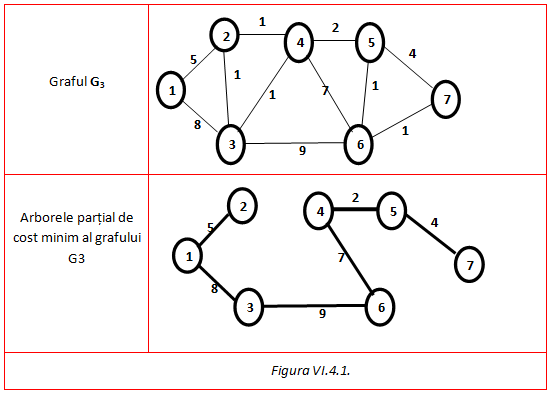
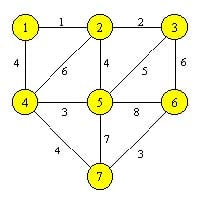
Se dă un graf neorientat g u x conex ponderat cu n noduri. Un arbore parțial al unui graf neorientat conex poate fi definit ca un graf parțial conex cu număr minim de muchii sau un graf parțial aciclic cu număr maxim de muchii. 7 3 7 4 7 9 7 6 9 8 1 3 1 2 si 2 5 suma costurilor acestor muchii este 37 solutia nu este neaparat unica. Dat fiind un graf neorientat conex se numeste arbore parțial al grafului un graf parțial cu proprietatea că este arbore intuitiv un arbore parțial este un arbore obținut prin eliminarea unor muchii din graf.

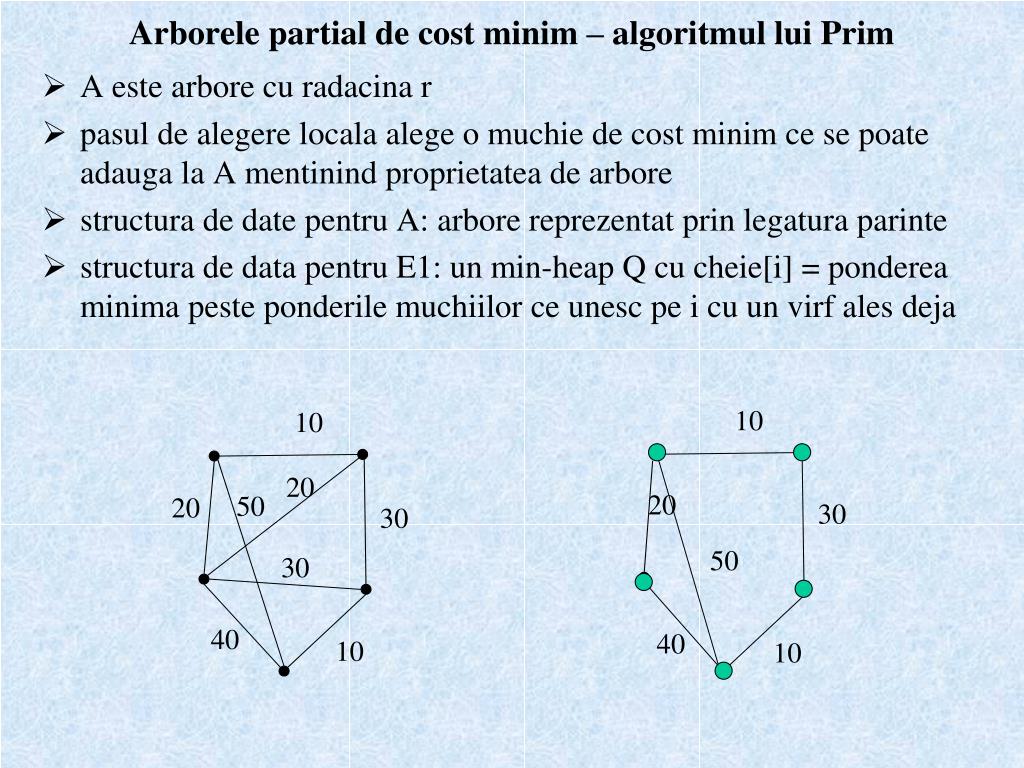
Datele de intrare se vor citi din fisierul text graf in care conţine pe prima linie două numere naturale n numărul de noduri şi m numărul de muchii iar pe următoarele m linii triplete de numere naturale x y cost care reprezintă muchia x y şi. Arbori de cost minim. Pentrul graful g conex cu funcția de cost c exista un graf partial. Desi solutia optima ar parea la prima vedere introducerea tuturor celor 3 muchii acest lucru nu este posibil deoarece s ar crea un ciclu.

Dacă din acesta se elimina muchii astfel încat să se obțină un arbore parțial al carui cost sa fie minim acesta se numește arbore partial de cost minim. Fie urmatoarea problema concreta. Arbore partial de cost minim. 10 fluxuri în reţea.

Model de prezentare a lucrării de laborator.